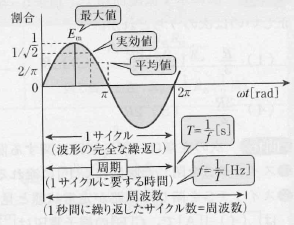
交流回路では、電圧と電流が時間とともに周期的に変化する。
このため、電圧降下は単に抵抗だけでなく、回路の持つリアクタンスという要素も考慮する必要がある。
リアクタンスには、誘導性リアクタンスと容量性リアクタンスの2種類がある。
交流回路のインピーダンス
交流回路における抵抗、誘導性リアクタンス、容量性リアクタンスを総合したものがインピーダンス (Impedance: Z) インピーダンスは、交流電流の流れにくさを表す量であり、単位は抵抗と同じオーム [Ω] で、
一般的に複素数で表現される。
インピーダンスの計算方法
インピーダンス (Z) は、抵抗成分 (R)、誘導性リアクタンス (X_L)、容量性リアクタンス (X_C) を
用いて次のように表される。
Z=R+j(XL−XC)
※(j) は虚数単位
インピーダンスの大きさ(絶対値)(|Z|) は、
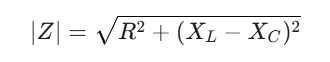
となる。
各成分による電圧降下
交流回路における電圧降下は、電流 (I) がこのインピーダンス (Z) を流れることによって生じる。
オームの法則を交流回路に拡張した形で表すと、
V=I×Z
ここで、V,I,Zはそれぞれ電圧、電流、インピーダンスの複素数表現(フェーザ)となる。
電圧降下は、インピーダンスの両端にかかる電圧であり、
Vd=I×Z=I×(R+j(XL−XC))=IR+jI(XL−XC)
となる。
それぞれの成分による電圧降下
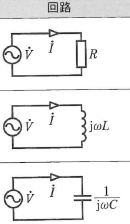
- 抵抗による電圧降下 ((\mathbf{I}R)): 電流と位相が同じ。直流回路と同様の原理で発生する。
- 誘導性リアクタンスによる電圧降下 ((jXL)): 電流に対して位相が (90°) 進んでいる。コイル(インダクタ)は、電流の変化を妨げる性質があり、交流電流に対して抵抗のような働きをする。この抵抗成分が誘導性リアクタンスとなる。
- 容量性リアクタンスによる電圧降下 ((-jXC)): 電流に対して位相が (90°) 遅れる。コンデンサは、電圧の変化を妨げる性質があり、交流電流に対して抵抗のような働きをする。この抵抗成分が容量性リアクタンスとなる。
リアクタンスと周波数の関係
誘導性リアクタンス (X_L) と容量性リアクタンス (X_C) は、
交流の周波数 (f) [Hz] と、インダクタンス (L) [H]、キャパシタンス (C) [F] によって決まる。
XL=2πfL=ωL XC=2πfC1=ωC1
※ω(2πf)は角周波数 [rad/s]のこと 。
位相差の影響
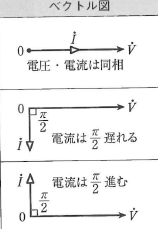
交流回路における電圧降下の特徴的な点は、電流と各成分による電圧降下の間に位相差が存在することである。
抵抗による電圧降下は電流と同位相だが、誘導性リアクタンスによる電圧降下は電流より (90°) 進み、
容量性リアクタンスによる電圧降下は電流より (90°) 遅れる。
したがって、回路全体の電圧降下は、これらの各成分による電圧降下を単純に足し合わせたものではなく、位相を考慮したベクトル和として計算する必要がある。

力率の影響

交流回路においては、電圧と電流の位相差を表す力率 も電圧降下に影響を与える。
力率が低い(位相差が大きい)場合、同じ有効電力に対してより大きな電流が流れるため
電圧降下も大きくなる傾向がある。





コメント